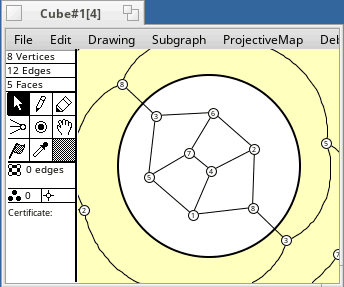
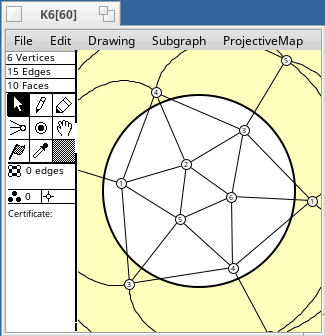
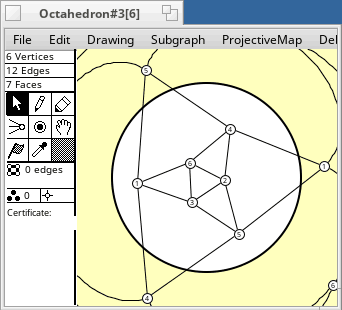
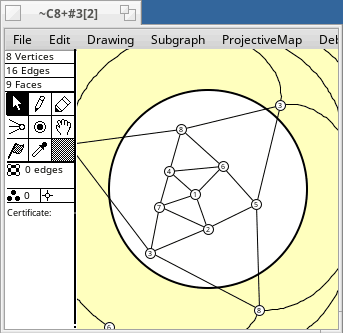
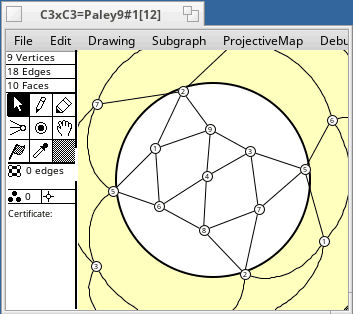
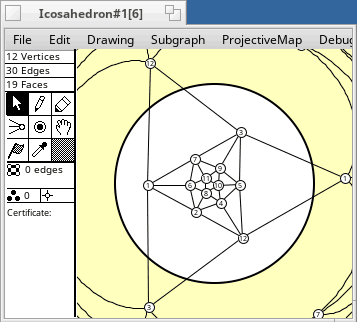
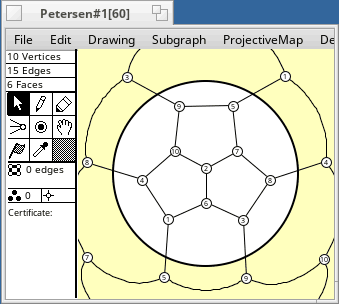
The table following is a list of projective plane embeddings of some small graphs, most of which are vertex transitive. Only 2-cell embeddings are considered. Most vertex transitive graphs are not projective planar. Except for the cycles C_n, which are always projective, vertex transitive graphs with at most 16 vertices which do not appear in the table are not projective planar.

The naming of the graphs is described here. The embeddings were generated by software. n, ε, f mean the numbers of vertices, edges, and faces.

All projective embeddings are non-orientable, because the projective plane is non-orientable. The order of the graph's automorphism group is in square brackets, eg. [24]. The embeddings have subgroups as automorphism groups. Their orders are divisors of the group order, and are listed after the group order.
Some diagrams follow the tables.

Download a text file containing these embeddings.

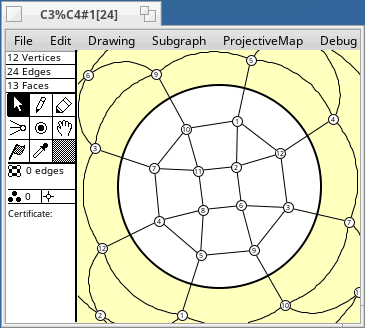
[The graph named C₃%C₄ is a kind of "Möbius product" of C₃ and C₄. Its projective embedding looks nearly identical to the torus embedding of C₃xC₄. It can also be derived as the antipodal graph of trunc(K₄).]