Projective Plane Obstructions

Last update=30 May, 2018

A non-planar graph is one which cannot be embedded in the plane. Kuratowski's theorem says that a graph G is non-planar iff it contains a subgraph topologically equivalent to one of K_3,3 or K₅. In terms of graph minors this can be expressed by saying that G has no minor K_3,3 or K₅. This is because a graph minor of G is any graph that can be formed by deleting vertices or edges of G, or by contracting edges of G. So we can say that K_3,3 and K₅ are minor-order obstructions to planarity. Thus there are two graphs that are minor-order obstructions to planarity, because they are the unique two minimal non-planar minors.

A non-projective graph is one which cannot be embedded in the projective plane. There are 35 minor-order obstructions to projective planarity. They were found by Glover, Huneke and Wang in 1979. Any graph that has one of these as a minor is non-projective. The smallest has 7 vertices, and the largest has 12 vertices (2K₆). Some of them are shown below.

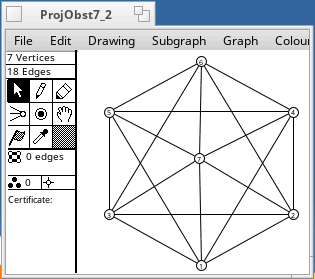
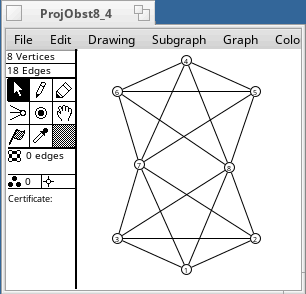
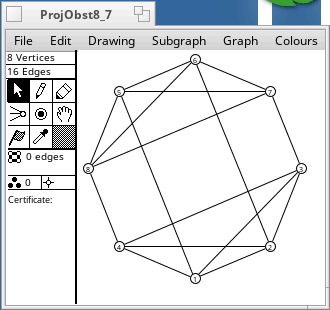
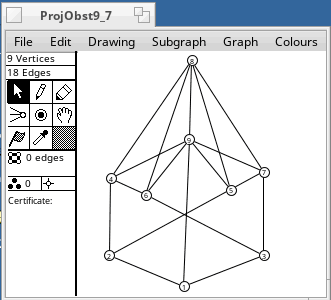
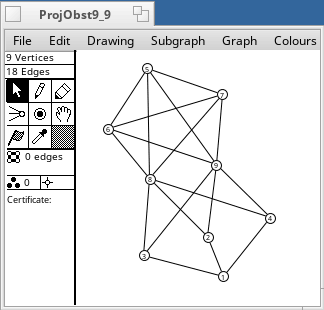
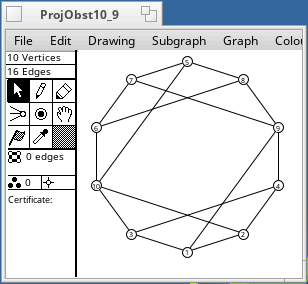
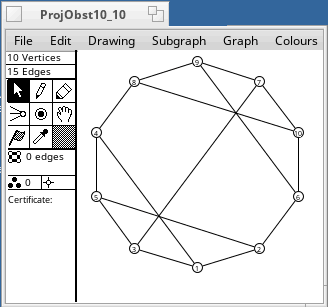
These graphs were drawn from adjacency matrices supplied by Wendy Myrvold. It is still not known how many minor-order obstructions there are for the torus. Myrvold has found tens of thousands, and it is not known whether her list is complete.

Download: