Last update=4 Sept, 2021

B. Grünbaum, Configurations of Points and Lines, American Mathematical Society, 2009.
T. Pisanski and B. Servatius, Configurations from a Graphical Viewpoint, Birkhauser, 2013.
The smallest (n3) configuration has n=7, shown below.
- L1 L2 L3 L4 L5 L6 L7
- 1 2 3 4 5 6 7
- 2 3 4 5 6 7 1
- 4 5 6 7 1 2 3
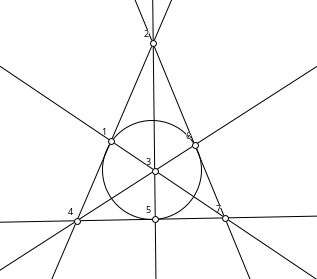
One line is drawn as a circle, because it is not possible to represent each Li as a straight line. There is exactly one configuration (73), and one configuration (83), which is known as the Möbius-Kantor configuration. It also cannot be drawn with straight lines, but can be drawn with one line represented as a circle.
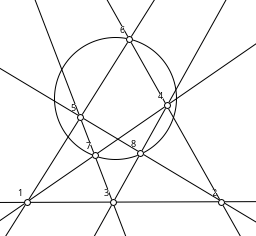
When n=9, there are three configurations (93), and they can all be drawn such that every "line" is a straight line. When this is possible, the configuration is said to be geometric or realizable.
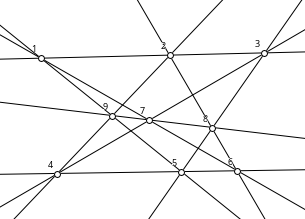
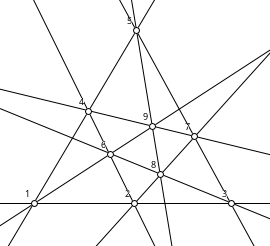
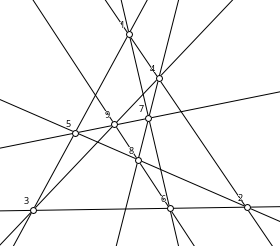
There are ten configurations (103), of which nine are geometric. One is non-geometric, it is known as the anti-Pappian. A diagram of it follows !
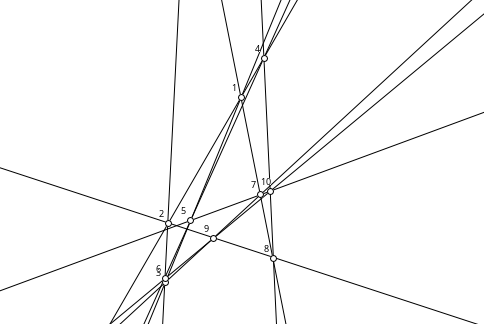
There are 31 configurations (113), originally found by Martinetti (1887). And there are 229 configurations (123), originally found by Daublebsky von Sterneck (1888). The (113) and (123) configurations are all geometric. The numbers of configurations are known up to n=19, found by computer by Betten, Brinkman and Pisanski. Grünbaum has conjectured that if a configuration is geometric, then it has a drawing in the plane such that all point and line coordinates are rational. Bokowski, Sturmfels and White have shown that this is true when n ≤ 12. Recent work (see below) shows that all (133) configurations are also geometric and rational. It is not yet known whether there are any other non-geometric configurations that are non-trivial. Note that a configuration must be connected, and must satisfy certain other basic properties described in Grünbaum's book.
Recently an algorithm (see W. Kocay, "One-point extensions in (n3) configurations", Ars Math. Contemp. 10 (2016), 291-322 and "Coordinatizing (n3) configurations", Ars Math. Contemp. to appear) shows how to construct extensions of a configuration (n3) to ((n+1)3). If the (n3) has an integer coordinatization, then the algorithm can usually find an integer coordinatization of the ((n+1)3) configuration, extended from the (n3), when one exists. Using this algorithm, integer coordinatizations of all 2036 configurations (133) have now been constructed. Thus all (133)'s are geometric and all are rational. One noticeable feature of the integer coordinatizations is that the number of digits in the point and line coordinates grows very rapidly with increasing n.
Coordinates
It is convenient to use homogeneous coordinates in the plane for the points and lines of a geometric configuration. Then point i with coordinates Pi and line j with coordinates Lj are incident if and only ifPi ⋅ Lj = 0. For example, the Pappus configuration, a (93), is given by the table following.
- L1 L2 L3 L4 L5 L6 L7 L8 L9
- 1 4 1 1 2 2 3 3 7
- 2 5 5 6 4 6 4 5 8
- 3 6 9 7 9 8 7 8 9
| i | Pi | Li | |
|---|---|---|---|
| 1 | (1,0,1) | (0,1,0) | |
| 2 | (0,0,1) | (1,0,1) | |
| 3 | (1,0,0) | (1,1,-1) | |
| 4 | (-1,1,1) | (1,0,-1) | |
| 5 | (1,-2,-1) | (1,1,0) | |
| 6 | (0,1,0) | (1,0,0) | |
| 7 | (1,1,1) | (0,1,-1) | |
| 8 | (0,2,1) | (0,1,-2) | |
| 9 | (1,-1,0) | (1,1,-2) |
A point (x, y, z) with z = 0 is a point at infinity.
Text Files
Some text files of the small configurations can be downloaded here. They are in the Haiku G&G format. The naming of the (103)'s corresponds to that in Grünbaum's book. The naming of the others is based on the order in which they were generated by the software. The order of the collineation group is shown in square brackets as part of the configuration's name, eg. (10,3)#10[120sd] means that configuration (10,3)#10 has a collineation group of order 120, and that it is self-dual.Download:
- some integer coordinatizations of the three (93) configurations.
- some integer coordinatizations of the ten (103) configurations
(+ the antiPappian). - some integer coordinatizations of the 31 (113) configurations.
- some integer coordinatizations of the 229 (123) configurations.
- some integer coordinatizations of the 2036 (133) configurations.
The Anti-Pappian
The anti-Pappian has a very interesting construction. Choose four points P1, P2, P3, P4 in general position. They determine six lines PiPj, where 1 ≤ i < j ≤ 4. Choose four lines L1, L2, L3, L4 in general position, such that no point Pi is on a line Lj. The four lines determine six points of intersection LiLj, where 1 ≤ i < j ≤ 4. Each line PiPj currently contains two points, and each point LiLj is currently on two lines. Place point LiLj on line PiPj. The result is the configuration (103) known as the anti-Pappian. Clearly the symmetric group S4 permutes the points and lines as collineations.

 Back to the Groups & Graphs home page.
Back to the Groups & Graphs home page.