Last update=6 Feb, 2009

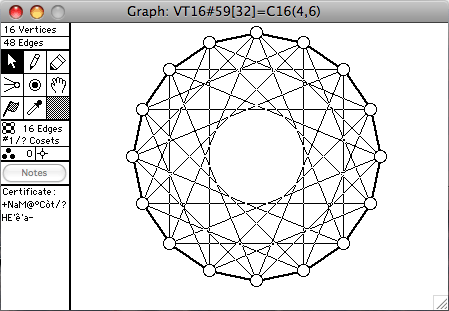
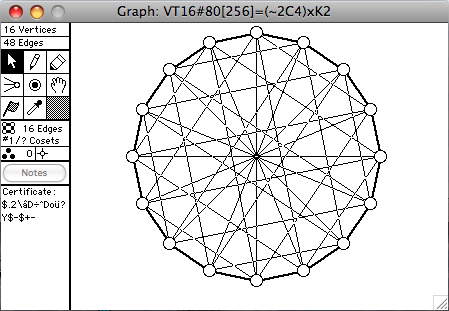
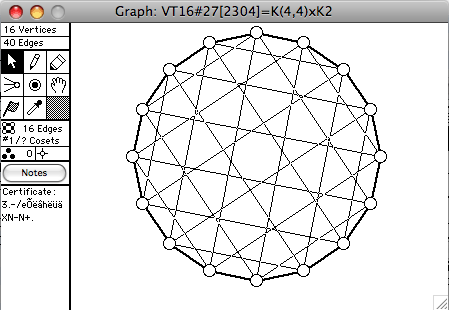
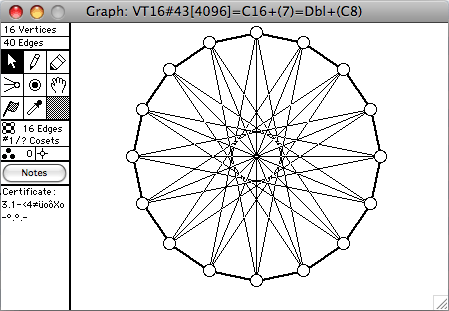
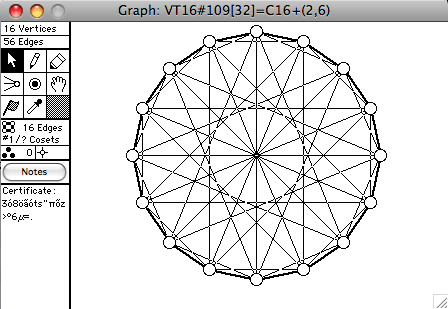
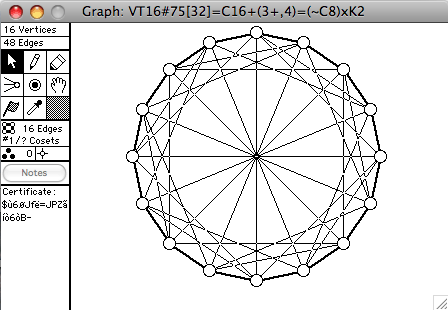
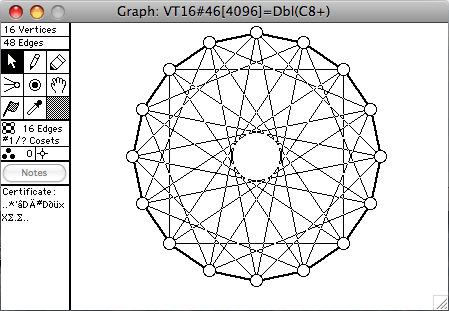
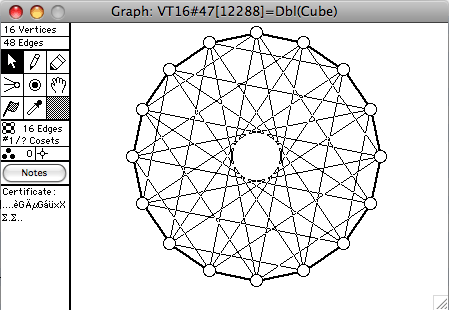
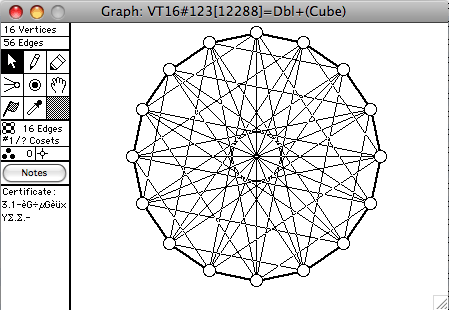
There are 272 connected vertex-transitive graphs on 16 vertices. A selection of them is shown here. The order of the automorphism group is given in square brackets in each window's title.

Notation:

• C_n means the cycle of length n
• C_n⁺ means the cycle of length n with diagonals
• C_n(k)  means the cycle of length n with chords of length k
• C_n(k⁺)  means the cycle of length n with chords of length k from every second vertex
• ~G   means the complement of G
• 2G   means two disjoint copies of G
• GxH   means the direct product of G and H
• L(G)   means the line graph of G
• Q₃ and Q₄    mean the graphs of the cube and hypercube
• Dbl(G)   means the double of G. Make 2 copies of G, call them G₁ and G₂. If uv is an edge of G, then u₁v₂ and v₁u₂ are also edges of Dbl(G)
• Dbl⁺(G)   means the double of G, with the additional edges u₁u₂
• BiDbl(G)   means the bipartite double of G. Make 2 copies of V(G), call them V₁ and V₂. If uv is an edge of G, then u₁v₂ and v₁u₂ are edges of BiDbl(G)
• BiDbl⁺(G)   means the bipartite double of G, with the additional edges u₁u₂ for each u in V(G)
• SR(n,k,λ,μ) means a strongly regular graph with n vertices, degree k, and parameters λ and μ

A number of the transitive graphs on 16 vertices can be constructed from 2Q₃, two copies of the cube. Then add additional edges. For example Q₄, the Clebsch graph, and the Shrikande graph can all be constructed in this fashion. It is possible to chose the vertices of 2Q₃ in four groups of four, and induce K₄'s on these subsets, etc., to obtain a number of vertex-transitive graphs.

    Back to the Groups & Graphs home page.