Last update=29 May, 2006

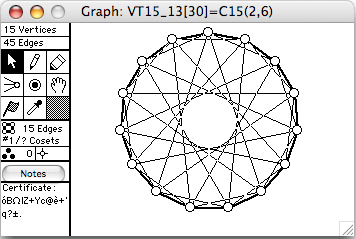
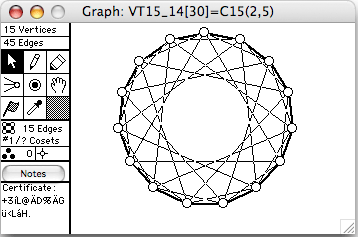
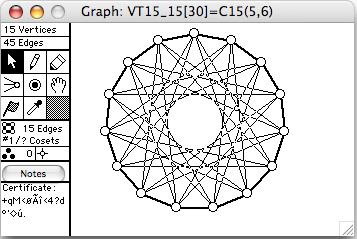
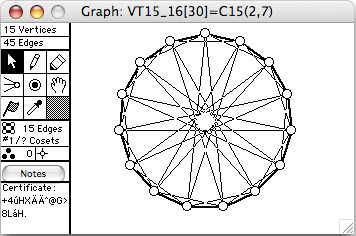
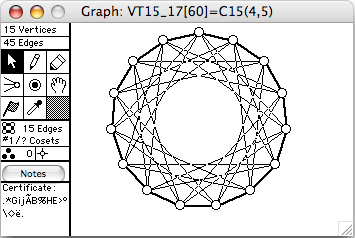
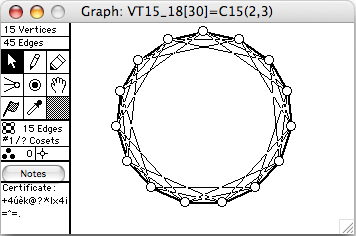
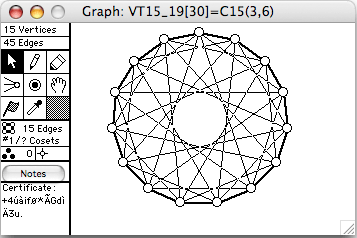
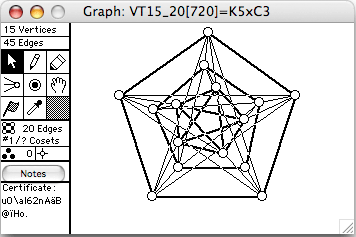
There are 44 connected vertex-transitive graphs on 15 vertices. The 12 of degree 6 (45 edges) are shown here. The order of the automorphism group is given in square brackets in each window's title.

Notation:

• C_n means the cycle of length n
• C_n⁺ means the cycle of length n with diagonals
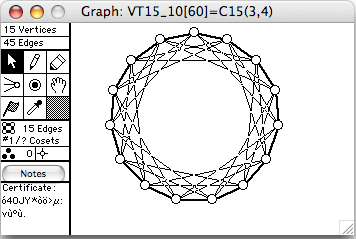
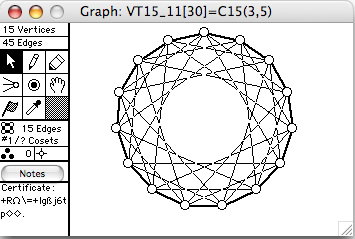
• C_n(k)  means the cycle of length n with chords of length k
• C_n(k⁺)  means the cycle of length n with chords of length k from every second vertex
• ~G   means the complement of G
• 2G   means two disjoint copies of G
• GxH   means the direct product of G and H
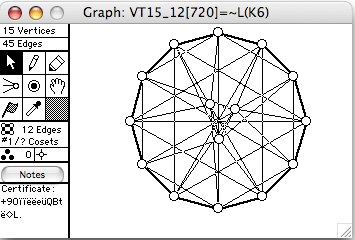
• L(G)   means the line graph of G
• Dbl(G)   means the double of G. Make 2 copies of G, call them G₁ and G₂. If uv is an edge of G, then u₁v₂ and v₁u₂ are also edges of Dbl(G)
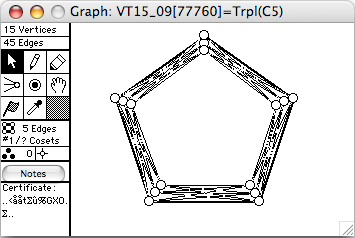
• Trpl(G)   means the triple of G. Make 3 copies of G, call them G₁, G₂ and G₃. If uv is an edge of G, then u₁v₂, u₁v₃, u₂v₁, u₂v₃, u₃v₁ and u₃v₂ are also edges of Trpl(G). This is a special case of the lexicographic product.

The complements of the graphs shown here are:

VT15_21 = ~C₁₅(2,6)

VT15_22 = ~C₁₅(2,3)

VT15_23 = ~C₁₅(3,6)

VT15_24 = ~C₁₅(3,4)

VT15_25 = ~C₁₅(2,5)

VT15_26 = ~C₁₅(2,4)

VT15_27 = ~K₅xC₃

VT15_28 = ~C₁₅(5,6)

VT15_29 = L(K₆)

VT15_30 = ~C₁₅(4,5)

VT15_31 = ~C₁₅(3,5)

VT15_32 = ~Trpl(C₅)

    Back to the Groups & Graphs home page.