Last update=20 May, 2006

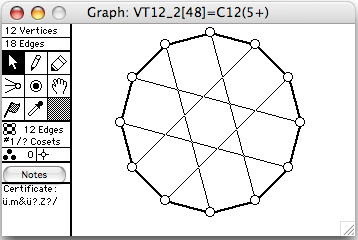
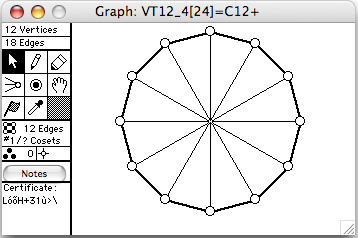
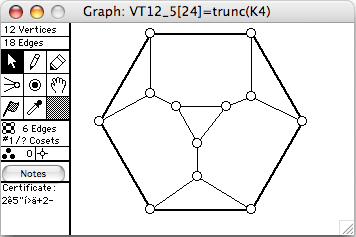
There are 64 connected vertex-transitive graphs on 12 vertices. The four of degree 3 (hence 18 edges) are shown here. The order of the automorphism group is given in square brackets in each window's title.
Notation:
- Cn means the cycle of length n
- Cn+ means the cycle of length n with diagonals
- Cn(k) means the cycle of length n with chords of length k
- Cn(k+) means the cycle of length n with chords of length k from every second vertex
- ~G means the complement of G
- 2G means two disjoint copies of G
- GxH means the direct product of G and H
- Prism(m) means CmxK2, ie, two cycles with corresponding vertices joined by a matching
- trunc(G), where G is planar, means to truncate G, ie, replace each vertex of degree k by Ck
C12 (=VT12_1) is not shown here. The complements of the graphs shown here, and the complements of the disconnected transitive graphs are:
- VT12_52 = ~2Prism(3)
- VT12_53 = ~3K4
- VT12_54 = ~trunc(K4)
- VT12_55 = ~(C6xK2)
- VT12_56 = ~C12+
- VT12_57 = ~C12(5+)
- VT12_58 = ~2K3,3
- VT12_59 = ~4K3
- VT12_60 = ~C12
- VT12_61 = ~2C6
- VT12_62 = ~3C4
- VT12_63 = ~6K2
- VT12_64 = K12
- VT12_53 = ~3K4
 |
 |
 |
 |