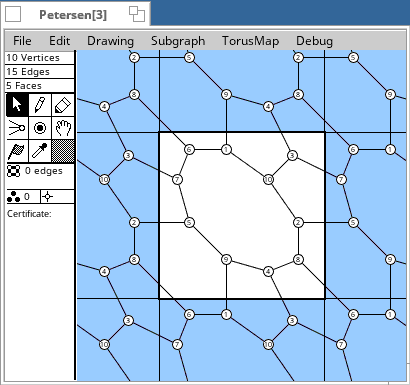
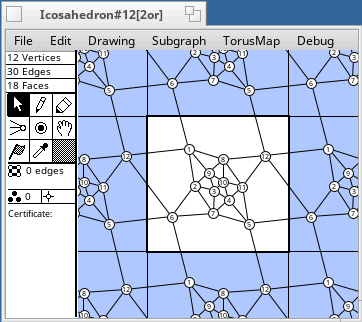
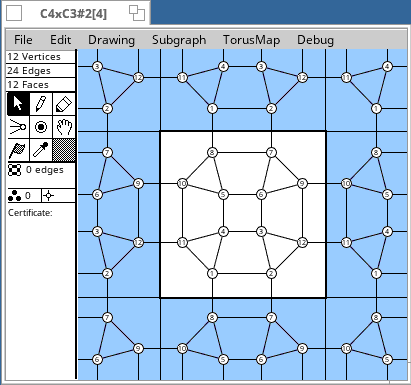
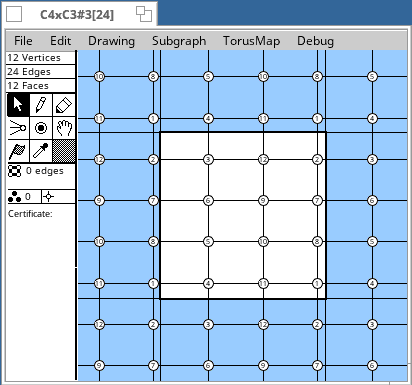
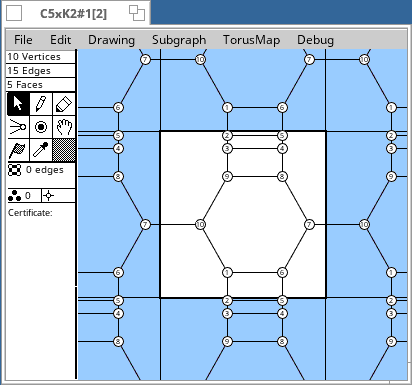
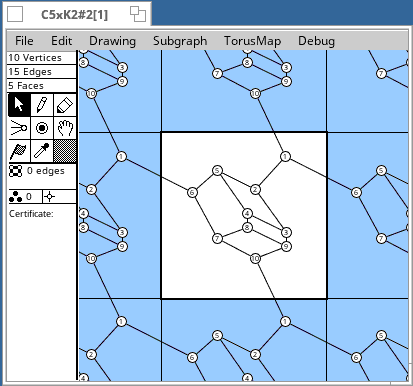
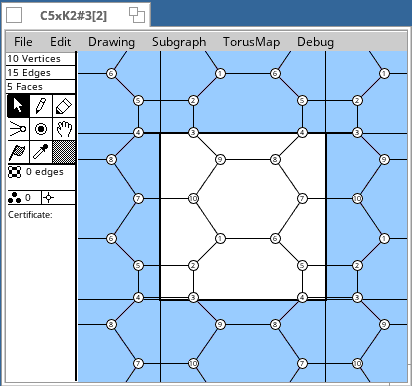
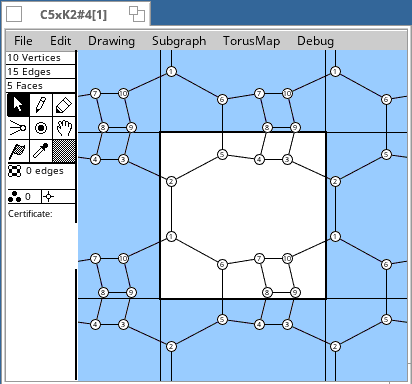
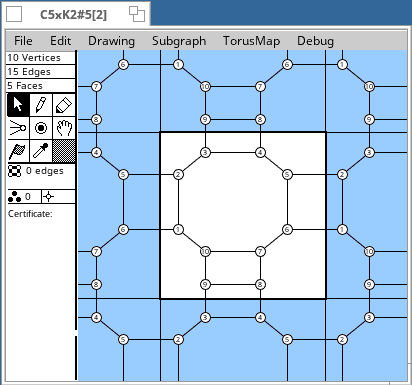
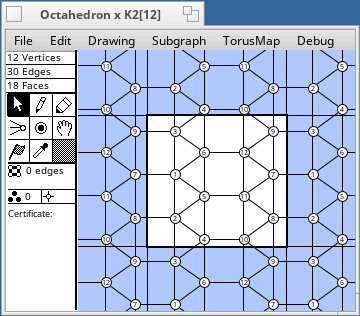
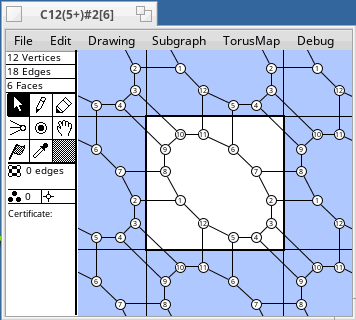
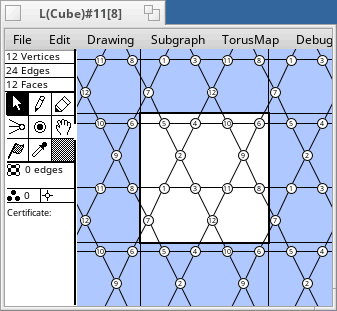
Torus Maps
Last update=8 Aug, 2020

A table of torus embeddings of some small graphs appears in
A. Gagarin, W. Kocay, and D. Neilson, "Embeddings of Small Graphs on the Torus" (2001), (260K) CUBO 5(2003), pp. 251-171.
The software that generated the original embeddings missed several embeddings. The condition that controls the loop was incorrect, causing the loop to sometimes stop too soon. The corrected numbers of embeddings are shown in the tables following. The graphs with corrected entries are marked with [*] in the last column.
The naming of the graphs is described here.
n, ε, f mean the numbers of vertices, edges, and faces.
Only 2-cell embeddings are considered.
Some embeddings are orientable and some are non-orientable.
An embedding is orientable if flipping it over results in a non-isomorphic embedding.
Otherwise it is non-orientable. Orientability is indicated in the graph name, eg.,
[12or] following the name means an orientable embedding with a group of order 12. The non-orientable embeddings have no special indication. Vertex transitive graphs with at most 12 vertices
which do not
appear in the table are not embeddable on the torus.
A group order like [24] in the table means that the graph has an automorphism group of order 24. The embeddings have subgroups as automorphism groups. Their orders are divisors of the group order, and are listed after the group order. Δ means a triangulation of the torus. Some diagrams follow the tables.
Individual files of distinct embeddings can be downloaded by clicking on the hilighted graph names. The unhilighted files are not yet available.
Download a text file containing all the embeddings available.