Sphere Maps
Last update=30 Apr, 2018

A graph can be embedded on the sphere iff it can be embedded on the plane. However, on the sphere, there is no outerface.
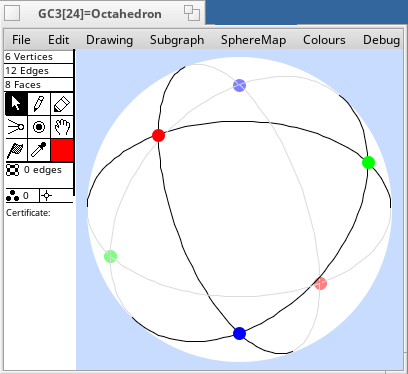
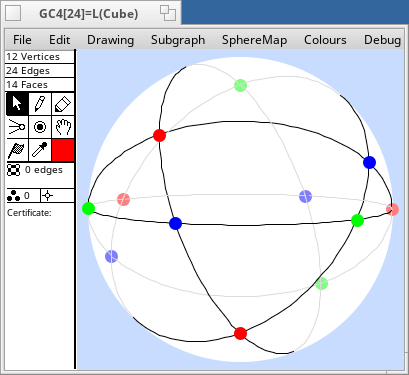
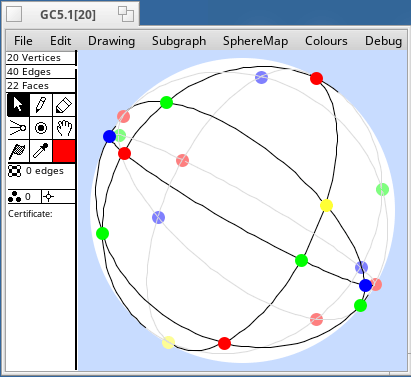
A very interesting class of sphere maps is the great circle graphs. These are graphs constructed from n great circles on the sphere, such that no three great circles are concurrent. The vertices are the intersections of the great circles. Each vertex has degree four. A great circle graph with n great circles has n(n-1) vertices and 2n(n-1) edges.
When n= 3, 4, or 5, there is a unique great circle graph. When n=6 there are four. Then the number of distinct great circle graphs begins to grow very fast.
Stan Wagon has conjectured that all great circle graphs can be coloured in three colours.
When n=3, the unique great circle graph is the graph of the octahedron. When n=4, the unique great circle graph is the line graph of the cube. In the pictures below, the number in square brackets after the name of the graph is the order of its automorphism group.